Summer School on Geometric and Algebraic Combinatorics Paris, 17-28 June 2019

Description

This two-week summer school will present an overview of a selection of topics in the crossroads between geometry, algebra, and combinatorics. It will consist of four one-week mini-courses given by leading experts, complemented with supervised exercise sessions, lectures by invited researchers, and research presentations by junior participants. The school is aimed at young researchers in geometric and algebraic combinatorics and related fields, although any interested researcher is welcome to participate. We expect the school to be an opportunity to bring together researchers from different backgrounds and foster new interactions. This school is part of the ongoing ANR project CAPPS.

Courses

Confirmed lecturers:

Federico Ardila (San Francisco State University & Universidad de los Andes)
Geometry of Matroids
Martina Juhnke-Kubitzke (University of Osnabrück)
Algebraic and combinatorial aspects of face numbers and Stanley-Reisner rings
Isabella Novik (University of Washington)
Combinatorial and topological aspects of face numbers and Stanley-Reisner rings
Bernd Sturmfels (University of California at Berkeley & Max Planck Institute for Mathematics in the Sciences Leipzig)
Polyhedral Subdivisions in Non-Parametric Statistics

News

08/04/2019 Registration is open!

Important dates

~~Support application deadline: January 30th, 2019.~~
~~Application for participation deadline: February 27th, 2019.~~
~~Contributed talk submission deadline: February 27th, 2019.~~
[updated] Early registration deadline: April 25th, 2019 (if not complete earlier).
Registration deadline: May 29th, 2019 (if not complete earlier).
Summer school: June 17-28, 2019.

Application for participation and registration

Due to the limited capacity of the lecture rooms, only participants who applied for participation are allowed to register. The application deadline was February 27th, 2019 and decisions were communicated in March. If you want to participate and did not apply, contact the organizers to be put on the waiting list.
If your application was accepted, and your registration fee is not covered by the school, please register here . You will first be asked to preregister and to choose which weeks you want to attend the summer school. Once you pass this step and your preregistration is validated by the organizing committee, you will receive a link to proceed to the payment.
The registration fees (except those exempted from financial support of the school) are:

100€/week for early registration before April 25th, 2019.
150€/week for registration before May 29th, 2019.

Registration fees only cover coffee breaks. Accommodation and meals are at the charge of the participants.

To prevent phishing attacks, note that the registration is done only through the Azur-colloque platform at the previous link. We will not contact you asking for your credit card details.

Contributed talk or poster submission

The program will include some research presentations by junior participants in two different formats:

25 min contributed talks (including questions), or
poster presentations.

The submission deadline was February 27th, 2019 and decisions were communicated in March.

Programme

Time	Monday 17	Tuesday 18	Wednesday 19	Thursday 20	Friday 21
9:00	Registration
9:30	Ardila (course)	Ardila (course)	Invited talk	Ardila (course)	Ardila (course)
10:00	Ardila (course)	Ardila (course)	Invited talk	Ardila (course)	Ardila (course)
10:30	Coffee break	Coffee break	Coffee break	Coffee break	Coffee break
11:00	Ardila (exercises)	Ardila (exercises)	Contributed talk	Ardila (exercises)	Ardila (exercises)
11:30			Invited talk
12:00			Invited talk
12:30	Lunch break	Lunch break	Lunch break	Lunch break	Lunch break
14:30	Contributed talk	Contributed talk	Contributed talk	Contributed talk	Contributed talk
15:00	Juhnke-Kubitzke (course)	Juhnke-Kubitzke (course)	Invited talk	Juhnke-Kubitzke (course)	Juhnke-Kubitzke (course)
15:30	Juhnke-Kubitzke (course)	Juhnke-Kubitzke (course)	Invited talk	Juhnke-Kubitzke (course)	Juhnke-Kubitzke (course)
16:00	Coffee break	Coffee break	Coffee break	Coffee break	Coffee break
16:30	Juhnke-Kubitzke (exercises)	Juhnke-Kubitzke (exercises)	Poster session	Juhnke-Kubitzke (exercises)	Juhnke-Kubitzke (exercises)
17:00
17:30

Time	Monday 24	Tuesday 25	Wednesday 26	Thursday 27	Friday 28
9:00	Registration
9:30	Sturmfels (course)	Sturmfels (course)	Invited talk	Sturmfels (course)	Sturmfels (course)
10:00	Sturmfels (course)	Sturmfels (course)	Invited talk	Sturmfels (course)	Sturmfels (course)
10:30	Coffee break	Coffee break	Coffee break	Coffee break	Coffee break
11:00	Sturmfels (exercises)	Sturmfels (exercises)	Contributed talk	Sturmfels (exercises)	Sturmfels (exercises)
11:30			Invited talk
12:00			Invited talk
12:30	Lunch break	Lunch break	Lunch break	Lunch break	Lunch break
14:30	Contributed talk	Contributed talk	Contributed talk	Contributed talk	Contributed talk
15:00	Novik (course)	Novik (course)	Invited talk	Novik (course)	Novik (course)
15:30	Novik (course)	Novik (course)	Invited talk	Novik (course)	Novik (course)
16:00	Coffee break	Coffee break	Coffee break	Coffee break	Coffee break
16:30	Novik (exercises)	Novik (exercises)	Problem session	Novik (exercises)	Novik (exercises)
17:00
17:30

Venue

The school will take place at the Jussieu Campus of the Faculty of Science & Engineering of Sorbonne Université. Lectures will be at room 15-25-104 at the 1st floor between towers 15 and 25.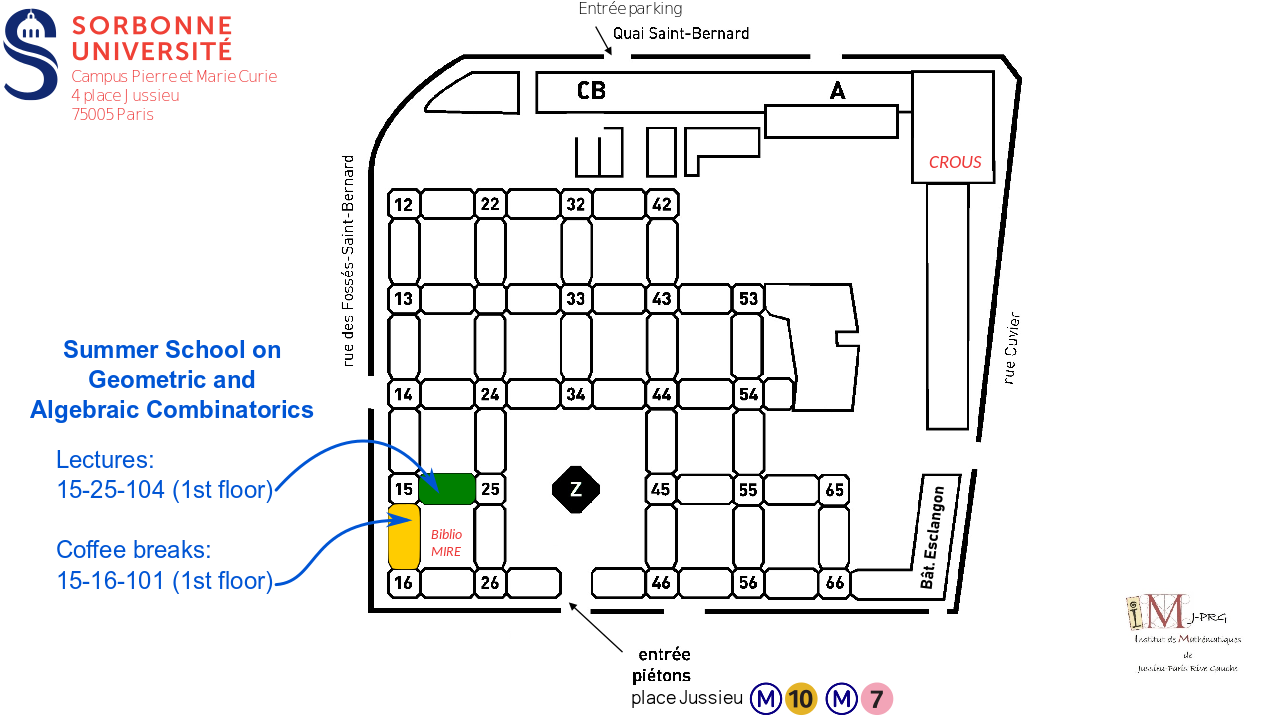

Organizers

Arnau Padrol (IMJ-PRG, Sorbonne Université)
Vincent Pilaud (LIX, École polytechnique)
Alfredo Hubard (LIGM, Université Paris-Est Marne-la-Vallée)
Julienne Belair (IMJ-PRG)

Contact

GACschool@imj-prg.fr

Related events

Conferences

FPSAC 2019, July 1–5, 2019, University of Ljubljana, Slovenia